Interquartile Range
What is the interquartile range?
The inter-quartile range shows the spread of a data set but is more accurate than using the range because it removes extremes. The inter-quartile range shows the spread of the middle 50 per cent of the data set because it removes the top and bottom 25%. It gives a better indication of how data is spread around the median value. The values are then divided into four equal groups or quartiles, where n is the number of values.
The upper quartile is the value that occurs in the following position:
(n+1) = Upper quartile (UQ)
4
The lower quartile is the value that occurs in the following position:
3(n+1) = Lower quartile (UQ)
4
The difference between the two values is known as the interquartile range. In the worked example below, we explore two approaches to calculating the interquartile range.
Calculating the interquartile range
The rainfall data below has been ranked in order and has been presented on a graph.
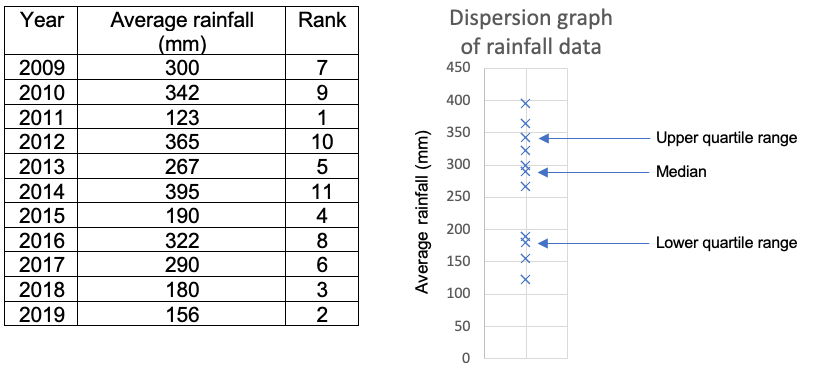
Approach 1
To work out the interquartile range for the rainfall data:
Lower quartile = 11+1 = 12 = 3
4
Third position = 180
Upper quartile = 3×12 = 36 = 9
4
Nineth position = 342
Therefore, the interquartile range is the difference between 180 and 342 = 162mm
Approach 2
Another way to calculate the interquartile range is to rank the data from lowest to highest e.g.
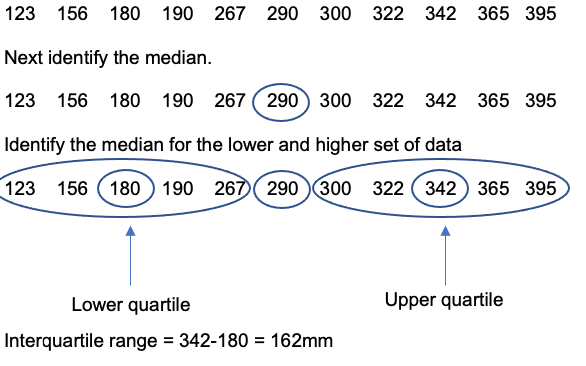
Statistical Techniques in Geography
Use the images below to explore related GeoTopics.



